Quantum Field Theory for the Gifted Amateur Exercise 1.4 The Subtle Dance of Field Variations and Dirac Delta Functions

In the previous article, we ventured into the enigmatic world of functional derivatives and unraveled their role in the ever-intriguing realm of Quantum Field Theory (QFT). Today, we’ll continue this exploration by diving into Exercise 1.4, which presents another layer of sophistication—how the Dirac delta function comes into play when we’re dealing with field variations.

Table of Contents

## The Problem Statement

Today’s quest revolves around two seemingly simple, yet profoundly intricate equations:

$\frac{\delta \phi(x)}{\delta \phi(y)}=\delta(x-y)$

$\frac{\delta \dot{\phi}(t)}{\delta \phi\left(t_0\right)}=\frac{\mathrm{d}}{\mathrm{d} t} \delta\left(t-t_0\right)$

The challenge is to prove these equations, which hold the secrets of how field variations interact at different points in space and time.

## The Solution Odyssey

### Problem 1: The Case of 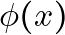$\phi(x)$ and $\phi(y)$

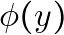
#### Step 1: Understanding the Variation

To understand how a variation in $\phi(y)$ affects $\phi(x)$ , we consider:

$\frac{\delta \phi(x)}{\delta \phi(y)} = \lim_{{\epsilon \rightarrow 0}} \frac{\phi(x) + \epsilon \delta(y - x) - \phi(x)}{\epsilon}$

#### Step 2: The Dance with the Dirac Delta

Notice that the term $\epsilon \delta(y - x)$ is responsible for the variation. As we let $\epsilon$ approach zero, this term transforms into $\delta(y-x)$ , leading us to:

$\frac{\delta \phi(x)}{\delta \phi(y)} = \delta(x - y) = \delta(y - x)$

### Problem 2: The Case of 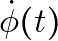$\dot{\phi}(t)$ and $\phi(t_0)$

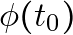
#### Step 1: Introducing Time Derivative

Here, we’re concerned with how a change in $\phi(t_0)$ affects the time derivative $\dot{\phi}(t)$ :

$\frac{\delta \dot{\phi}(t)}{\delta \phi\left(t_0\right)} = \lim_{{\epsilon \rightarrow 0}} \frac{\frac{d}{dt} \left( \phi(t) + \epsilon \delta(t_0 - t) \right) - \frac{d}{dt} \phi(t)}{\epsilon}$

#### Step 2: Unveiling the Result

Applying the derivative to the delta function, we arrive at:

$\frac{\delta \dot{\phi}(t)}{\delta \phi\left(t_0\right)} = \frac{d}{dt} \delta(t_0 - t)$

## Concluding Thoughts: The Quantum Ballet

This exercise has been a dance with the Dirac delta function, the brilliant invention of physicist Paul Dirac that serves as a mathematical representation of the idea of “point particles” in quantum theory. Our journey has led us to profound results that extend our understanding of the relationship between field variations at different points in space and time.

The equations we’ve proved today are not just mathematical curiosities; they form the building blocks of many advanced concepts in QFT. As we continue to peel back the layers of this fascinating subject, we’re reminded that the language of the universe is written in the dialect of mathematics, and each equation we solve is a step closer to understanding the cosmic dance of particles and fields.

Onward, to the next quantum mystery!