Quantum Field Theory (QFT) continues to be a fountain of bewitching complexity and awe-inspiring beauty. Our last foray into this enchanting realm dealt with functionals and their interaction with derivatives. Today, we venture further into this mathematical Eden by unraveling the second part of Exercise 1.3, extending our exploration into functionals involving both ![]() and
and ![]() .
.

Table of Contents
## The Exercise
For the functional ![]() , show that:
, show that:
![Rendered by QuickLaTeX.com \[ \frac{\delta H[f]}{\delta f(x)} = \frac{\partial g}{\partial f} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial g}{\partial f^{\prime}} \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-6bf69efe1b6663096b7759e54bdddcc5_l3.png)
## Step 1: Setting the Stage
The functional ![]() can be written as:
can be written as:
![Rendered by QuickLaTeX.com \[ H[f] = \int g\left(y, f, f^{\prime}\right) \, \mathrm{d}y \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-9952ac48f3e6e4b6ae277bb2d2177b27_l3.png)
To find the functional derivative ![Rendered by QuickLaTeX.com \frac{\delta H[f]}{\delta f(x)}](https://lazying.art/wp-content/ql-cache/quicklatex.com-d8b6c5517801a0be74fe73d922662bc1_l3.png) , we rely on the foundational definition:
, we rely on the foundational definition:
![Rendered by QuickLaTeX.com \[ \frac{\partial H[f]}{\partial f(x)} = \lim_{{\epsilon \to 0}} \frac{H[f(y) + \epsilon \delta(x-y)] - H[f(y)]}{\epsilon} \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-392600ae16bde4b48307c35a1ebbcccb_l3.png)
## Step 2: Tracing the Derivatives
Injecting ![]() into the definition, we obtain:
into the definition, we obtain:
![Rendered by QuickLaTeX.com \[ \begin{aligned} \frac{\partial H[f]}{\partial f(x)} &= \lim_{{\epsilon \to 0}} \frac{\int g(y, f(y) + \epsilon \delta(x-y), f^{\prime}(y) + \epsilon \delta'(x-y)) \, \mathrm{d}y - \int g(y, f(y), f^{\prime}(y)) \, \mathrm{d}y}{\epsilon} \\ &= \lim_{{\epsilon \to 0}} \int \left[\frac{\partial g}{\partial f} \delta(x-y) - \frac{\partial g}{\partial f^{\prime}} \delta'(x-y) \right] \, \mathrm{d}y \\ &= \frac{\partial g}{\partial f} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial g}{\partial f^{\prime}} \end{aligned} \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-a9b96ad6e5e20b0236dd0ac9cc0de014_l3.png)
In the poetic elegance of this equation, we confirm that ![Rendered by QuickLaTeX.com \frac{\delta H[f]}{\delta f(x)} = \frac{\partial g}{\partial f} - \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial g}{\partial f^{\prime}}](https://lazying.art/wp-content/ql-cache/quicklatex.com-0b02b2f5ffcd0bfed9c98999ff6d43ac_l3.png) .
.
## The Finale: Euler-Lagrangian Theorem
The result is not just an answer to an exercise but a fundamental expression of the Euler-Lagrangian equation, a cornerstone in the monumental edifice of quantum mechanics and classical field theory.
## Reflections
This has been another beguiling chapter in our expedition through Quantum Field Theory. The exercise illuminates how functionals and derivatives can dance together in complex choreography, adding texture to our understanding of physical laws at their most fundamental.
I am endlessly captivated by this quantum realm and invite you to join me in future explorations. Our understanding of this universe, so arcane yet so full of potential, only expands with each question we dare to ask.
## Delving Into the Intricacies: Understanding 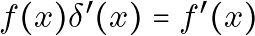
In our deep dive into functional derivatives and Quantum Field Theory, one mathematical expression may raise questions—why is ![]() ? Let’s look at this with more scrutiny.
? Let’s look at this with more scrutiny.
### The Dirac Delta Function and Its Derivative
The Dirac delta function ![]() is a distribution that “selects” a value of a function when integrated across a range containing zero. Its derivative
is a distribution that “selects” a value of a function when integrated across a range containing zero. Its derivative ![]() acts similarly, but rather than picking out a function value, it captures the function’s rate of change—its derivative—at that point.
acts similarly, but rather than picking out a function value, it captures the function’s rate of change—its derivative—at that point.
### Breaking Down the Integral
To understand ![]() , let’s consider an integral:
, let’s consider an integral:
![Rendered by QuickLaTeX.com \[ \int_{-\infty}^{\infty} f(x) \delta^{\prime}(x-a) dx \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-cd5303c55b9a583b594fbd13ceeef8ec_l3.png)
By integration by parts, ignoring boundary terms, and understanding that ![]() is a distribution, we get:
is a distribution, we get:
![Rendered by QuickLaTeX.com \[ - \int_{-\infty}^{\infty} f^{\prime}(x) \delta(x-a) dx = -f^{\prime}(a) \]](https://lazying.art/wp-content/ql-cache/quicklatex.com-a442dedc7ef37fbb1aea04194c260995_l3.png)
We see that the derivative of ![]() evaluated at
evaluated at ![]() is effectively “picked out” by the term
is effectively “picked out” by the term ![]() when integrated.
when integrated.
### Simplification for 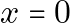
In our original equation ![]() , this is simply the specialized case when
, this is simply the specialized case when ![]() . Thus,
. Thus, ![]() and
and ![]() are interchangeable under the integral, validating the equation.
are interchangeable under the integral, validating the equation.
### Summary
The expression ![]() isn’t just a mathematical trick; it is a nuanced representation that shows how distributions like
isn’t just a mathematical trick; it is a nuanced representation that shows how distributions like ![]() and its derivatives interact with functions and their derivatives under an integral.
and its derivatives interact with functions and their derivatives under an integral.
As we push the boundaries of our understanding in Quantum Field Theory, such insights elevate our command of the subject, providing us with a fuller, more nuanced view of the mathematical landscape we traverse.
